|
|
考研数学的题型分三类:概念题、计算题和证明题。
只要把概念题锤炼至求同存异的层次、计算题锤炼至大道至简的层次并加上三大证明题的三种方法,140的分数并不是很难。关键在于你要确定自己现在在什么层次,并进行针对性训练。
针对考研数学的八大归纳总结是我对对考研数学的体会和理解,凝结了我对考研数学的思考,其包括概念、计算和证明题的简洁归纳。具有一力破十慧之效果。二归纳总结全部脱胎于以下我对于考研数学的理解。
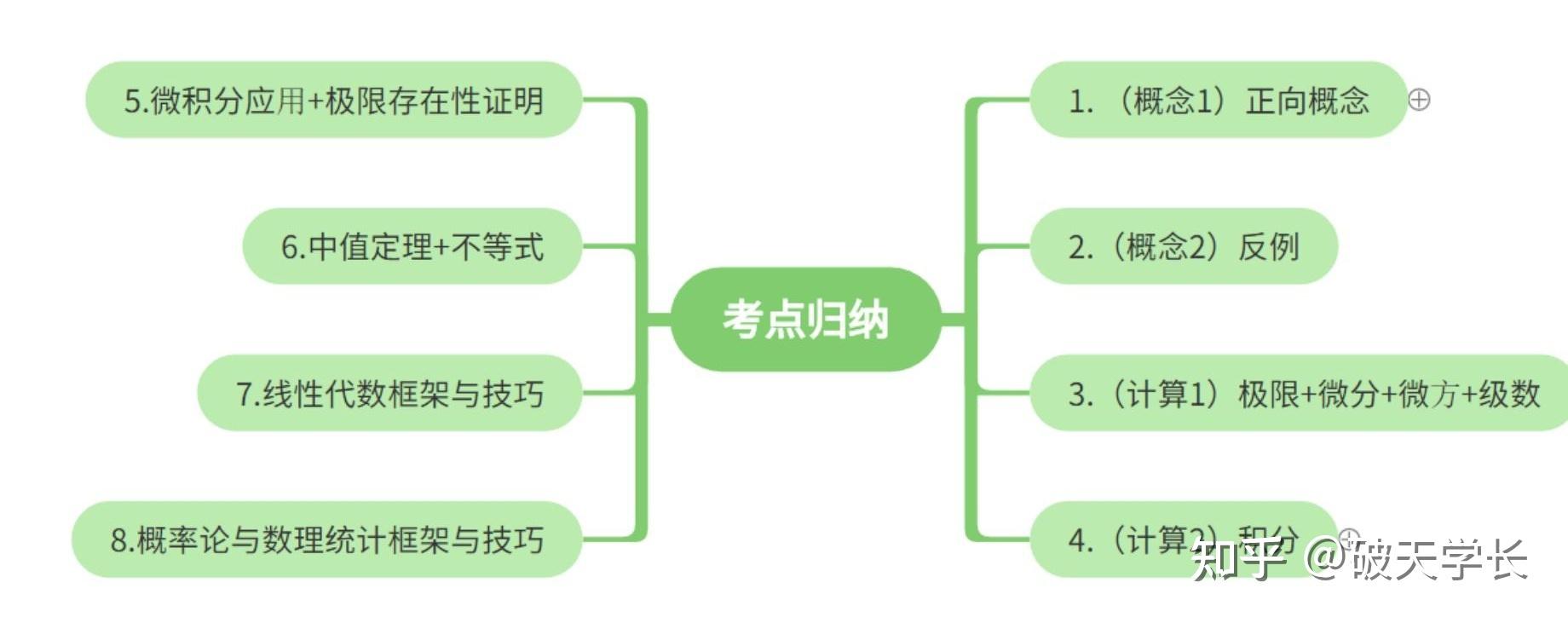
八大归纳总结
一、概念题
概念题既没有复杂的计算(计算壁垒)又没有曲折的思路(思路壁垒),当你对概念理解的足够深刻,那么自然而然就能做出来,反之,如果,你考试之前没有透彻的理解概念,一旦考场上出了相应深度的题型,就只能掷骰子了。高等数学的概念部分主要包括:
极限(函数极限、数列极限、无穷小、无界、无穷大)、微分(一元导数、多元微分概念)、积分(积分相关定义与条件、不定积分与原函数、反常积分敛散性、无穷级数敛散性)、微分方程解的性质四大部分。
实际上,概念题的学习一般有四个层次:
1.第一层次
一轮复习后,对基本概念存在粗浅、不严谨、淡化、甚至抵触的认识理解:
比如函数极限定义,很多同学一看到 \varepsilon-\sigma 语言就感到很陌生,更不要说理解了。
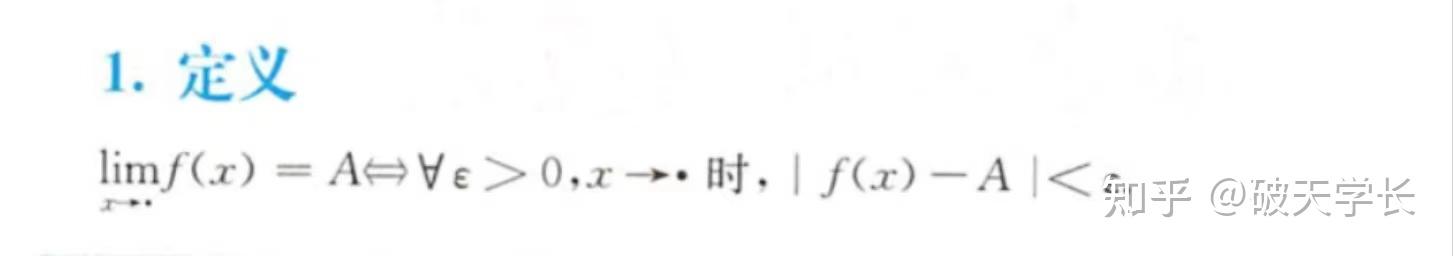
函数极限定义
2.第二层次
过强化训练,尤其是做过660的同学,在经过大量不同角度概念的题型的冲击后,对概念就会有了一些初步的理解,从具体的形式理解概念正是我们理解概念最有效的方式;但是,很多同学在这一阶段对于概念的理解还是片面的、碎片化的、边缘化的,形不成一个整体、核心、本质的概念的理解,一旦遇到从类没没遇到过的题型,就无法变通。
3.第三层次(求同存异)
也称之为求同存异的阶段,这一阶段很重要需要一定的韧性和经验才能顺利达到但这一阶段也是收获最多的阶段。
何为求同?求同就是最为核心的、最为本质的、最为简洁的归纳理解。不妨举两个例子:
比如大家都知道函数极限具有局部有界性、局部保号性和等式脱帽法三个最常用的性质,具体如下:

函数极限的局部有界性、局部保号性和等式脱帽法
如何你学会归纳总结,你会发现,等式脱帽法时更为本质的性质,因为,局部保号性和局部有界性都可以由等式脱帽法推导出来。
等式脱帽法——推——局部有界性:
给定极限 \lim_{x\rightarrow.}f(x)=A ,有等式脱帽法知 x\rightarrow.时, f(x)=A+\alpha,其中,\lim_{x\rightarrow .}\alpha=0 ;
因为, \left| \alpha \right|< 任意正常数(不妨给定设任意正常数为 \gamma ),所以,当 x\rightarrow.时 , \left| f(x) \right|<\left| A \right|+\gamma\leq M
所以,当 x\rightarrow.时 , f(x) 的取值围绕着A跳动,其跳动范围为无穷下 \alpha ,故 f(x) 必有界。 等式脱帽法——推——局部保号性:
给定极限 \lim_{x\rightarrow.}f(x)=A ,有等式脱帽法知 x\rightarrow.时,f(x)=A+\alpha,其中,\lim_{x\rightarrow .}\alpha=0 ;
有A>0, ,因此, f(x)=A+\alpha>0(易知,任意正常数A>\alpha) ;
当 f(x)\geq0时,A=f(x)-\alpha\geq0 . 很容易看出,局部保号性、局部有界性都可以通过等式脱帽法推导出来,这就是求同,将函数极限理解至以等式脱帽法为中心,进行辐射理解,这样在做概念题的的时候,只要涉及到函数极限,即便,你不知道有界性和保号性,仅仅凭借等式脱帽法,你也可以很容易的做出正确结论。
又或者是反常积分敛散性的问题
直接给出核心的反常积分敛散性判别的万能公式(具体可参照破天学长:反常积分敛散性判别的万能公式)
将任意反常积分化为标准型 \int_{}^{}\frac{1}{x^{\alpha}ln^{\beta}x}dx ,
(1)当 x\rightarrow 0(瑕积分),\begin{cases} \alpha<1 \\[2ex] \alpha=1,\beta>1\end{cases},收敛 ;
(2)当x\rightarrow \infty(无穷区间的反常积分),\begin{cases} \alpha>1 \\[2ex] \alpha=1,\beta>1\end{cases},收敛
(3)其他情况均发散!
(注意:此公式推导可参照我的14节课冲刺课,实际上,记住结论即可) -若反常积分 \int_{0}^{1}x^{a}(1-x)^{b}lnxdx 收敛,则可确定 a、b 。
万能公式法:
当x\rightarrow0^{+}时,有
x^{a}(1-x)^{b}lnx\sim\frac{1}{x^{-a}ln^{-1}x}
若关于 x=0 的瑕积分收敛,则 \alpha=-a<1, 即 a>-1 ;
当x\rightarrow1^{-}时,有
x^{a}(1-x)^{b}lnx\sim-\frac{1}{(1-x)^{-(b+1)}}
若关于 x=1 的瑕积分收敛,则 \alpha=-(b+1)<1, 即 b>-2 ;
综上所述,当a>-1,b>-2时使得反常积分 \int_{0}^{1}x^{a}(1-x)^{b}lnxdx收敛。 这样几乎所有的反常积分都可以通过这个公式进行求解,更进一步的,无穷级数的敛散性判别也有相应的万能公式来进行判别,如果你能归纳出这种结论,那么所有敛散性都将变得简单异常。
<hr/>何为求异?极限中函数极限与数列极限的异同处;微分中一元微分与多元微分异同处;积分中的反常积分敛散性与级数敛散性的异同处;积分中不定积分与定积分的异同处;积分中定积分、二重积分、三重积分的异同处;积分中一二型曲线曲面积分的异同处等等相似“同类型”概念的对比,你是否真的能够看清楚?
不妨举一个函数极限与数列极限的例子:

函数极限的局部有界性

数列极限的有界性
函数极限的有界性称之为局部有界性,而数列中的有界性称之为有界性,局部的差异在哪里?
对于函数极限来说,当 x\rightarrow x_{0}时 ,即自变量趋向于一点 x_{0} 时,极限是定义于去心邻域 (x_{0}-\varepsilon,x_{0})\cup(x_{0},x_{0}+\varepsilon),其中\varepsilon任意小的正常数 ,也就是说,函数极限的局部有界性,是指的这个非常小的去心领域内是有界,这个局部的去心邻域非常小,比你给出的任何一个具体的领域都小。
而数列极限来说,从表述来说,对所有的n,数列的每一项 x_{n} 他们都是有界的。这是因为在 n\rightarrow\infty时, x_{n}是有界的,而非无穷项,也就是任意一个有限项x_{n}都是一个数,所以有限项也是有界的,所以,数列极限的有界性是对于所有项都是有界的。如下这道真题:

由于 \lim_{n\rightarrow \infty}{a_{n}}=1 ,所以数列 a_{n} 是有界,所以,必然存在最大值和最小值。 所以,对比差异化概念,没能让你更清晰的理解概念,这是历年真题中特别容易考的考点。
4.第四层次(返璞归真)
可以称之为返璞归真的阶段,实际上,无论是辅导书给出的各种基本概念的基本性质(如极限的保号性局部有界性、等式脱帽法等等),还是我们对性质进行归纳总结的万能公式等等理解都是给予我们个人的理解对概念的剖析,是有失偏颇的,不够严谨的,最为正确严谨的概念理解永远是定义!我们在归纳总结的时候,求同存异的时候,为了保证理解的正确性雅瑶始终将定义放在手边,进行印证剖析。如函数极限的定义
这里面的每一个字都不是废话,每一个字都具有探讨的意义,每个人再经历过前三个阶段的理解后,再回过头看这函数定义的表述,你会发现,它把所有的性质都包括了,而至于每个人由于对概念理解层次的不同,又能解读出不同层次的理解,这就是定义的严谨性,正所谓,书读百遍其意自现,正是这个道理,所以,我希望每个同学都能把定义背下来,自然你就能够时刻剖析,深入理解,概念的问题也将会迎刃而解。
二、计算题
计算题存在计算壁垒,也是考研数学中占比分值最大的部分,高数中的计算题包括极限、微分(一员求导、多元微分、求极值等等)、积分(不定积分、定积分等等)、微分方程和无穷级数(展开和求和),这些计算题普遍存在类型繁多,计算方式也是五花八门,很多同学能够掌握其中最为常见易解的题型方法,一旦遇到稍微少见的题型和方法以及大计算量就会出现低级错误,甚至完全做不出来,这就是所谓计算壁垒。计算主要包括:极限、微分(一元高阶导数、多元微分、求极值)、积分(不定积分、定积分、二重积分、三重积分、一二型线面积分)、级数的展开和求和、微分方程五大部分。
计算题的复习也分三个层次:
1.第一层次
掌握基本常见的计算题型,一旦遇到少见、灵活或者计算量大的题型就容易出错;
2.第二层次
这一层次的已经可以把计算题型的所有基本方法都熟练至极,也不会犯低级错误,面对计算量大的题目也能很好的应对,但,针对近年来计算量越来越大的趋势,尤其是22年填空题都具有答题计算量的形式,也是有些捉襟见肘。
3.第三层次(大道至简)
在这一层次的学生,对待题目都归纳出较为通用的万能解法,具有一法通万法的实力,以不变应万变,面对高计算量仍能够游刃有余的解决题目。极限中的泰勒公式、多元微分求导的协同法、多元极值的分离法、抑或是积分学中的偏移放缩法,甚至是级数求和的递推法,这些方法一旦掌握,对于大计算量的题型来说是具有“毁灭性”打击效果的。
比如极限中的泰勒公式(具体参照破天学长:函数极限的最强解法——泰勒公式!!!):
1. I_{1}=\lim_{x \rightarrow 0}{\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt[3]{1+x}-\sqrt[3]{1-x}}}
一般解法是:换元法
令 \sqrt[6]{1+x}=m,\sqrt[6]{1-x}=n
则
I_{1}=\lim_{(m,n) \rightarrow (1,1)}{\frac{m^3-n^3}{m^2-n^2}}=\lim_{(m,n) \rightarrow (1,1)}{\frac{m^2+mn+n^2}{m+n}}=\frac{3}{2}
泰勒求解法:
I_{1}=\lim_{x \rightarrow 0}{\frac{1+\frac{x}{2}-(1-\frac{x}{2})+o(x)}{1+\frac{x}{3}-(1-\frac{x}{3})+o(x)}}=\frac{3}{2}
2. I_{2}=\lim_{x \rightarrow 1}({\frac{m}{1-x^m}-\frac{n}{1-x^n}})
一般解法是:因式分解法
I_{2}=\lim_{x \rightarrow 1}{[(\frac{m}{1-x^m}-\frac{1}{1-x})-(\frac{n}{1-x^n}-\frac{1}{1-x})]}
取 I_{21}=\frac{m}{1-x^m}-\frac{1}{1-x}, I_{22}=\frac{n}{1-x^n}-\frac{1}{1-x}
则 I_{21}=\frac{m}{1-x^m}-\frac{1+x+x^2+...+x^{m-1}}{1-x^m}
=\frac{(1-1)+(1-x)+(1-x^2)+...+(1-x^{m-1})}{1-x^m}=\frac{0+1+(1+x)+...+(1+x+x^2+...+x^{m-2})}{1+x+x^2+...+x^{m-1}}
故 \lim_{x \rightarrow 1}I_{21}=\frac{0+1+2+...+(m-1)}{m}=\frac{m-1}{2}
同理, \lim_{x \rightarrow 1}{I_{22}}=\frac{n-1}{2}
则 I_{2}=\lim_{x \rightarrow 1}{I_{21}}-\lim_{x \rightarrow 1}{I_{22}}=\frac{m-n }{2}
泰勒解法:
令x=t+1
则 则 I_{2}=\lim_{t \rightarrow 0}{\frac{m}{1-(1+t)^m}-\frac{n}{1-(1+t)^n}}=\lim_{t \rightarrow 0}{\frac{m-n+n(1+t)^m-m(1+t)^n}{[1-(1+t)^m][1-(1+t)^n]}}
=\lim_{t \rightarrow 0}{\frac{m-n+(n+nmt+\frac{nm(m-1)t^2}{2})-(m+mnt+\frac{mn(n-1)t^2}{2})+o(t^2)}{mnt^2+o(t^2)}}=\frac{m-n}{2}
亦或是二重极限(破天学长:二重极限的最强解法——极坐标代换法!!!):
二重极限
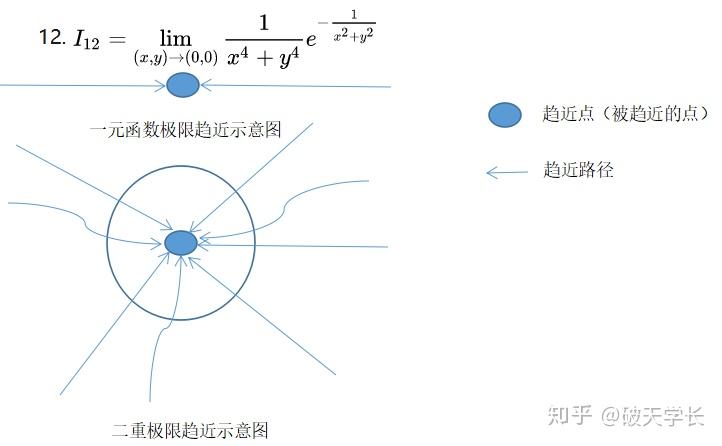
这是多么简单的一道题啊,但是辅导书的讲解你即便看完了,遇到一个新题,仍然是不会做,真是可笑啊!
例如:I_{2}=\lim_{(x,y) \rightarrow (0,0)}{\frac{xy^2}{x^2+y^4}}
辅导书解法:令 y=kx,则
I_{2}=\lim_{(x,y) \rightarrow (0,0)}{\frac{xy^2}{x^2+y^4}}=\lim_{x \rightarrow 0}{\frac{kx^3}{x^2+k^4x^4}}=\lim_{x \rightarrow 0}{\frac{kx^3}{x^2}}=0
k无论取什么,极限都是为0,极限就存在吗?
显然不是!
我们取另一种路径,即 y^2=x(没做过你能想的到吗?)
I_{2}=\lim_{(x,y) \rightarrow (0,0)}{\frac{xy^2}{x^2+y^4}}=\lim_{x \rightarrow 0}{\frac{x^2}{x^2+x^2}}=\frac{1}{2}
由于两个极限值分别是0和1/2.所以,极限不存在!
我的解法:令 x=rcos\theta ,y^2=rsin\theta, \theta\in(0,\pi)则
I_{2}=\lim_{(x,y) \rightarrow (0,0)}{\frac{xy^2}{x^2+y^4}}=\lim_{r \rightarrow 0^+}{\frac{r^2cos \theta sin\theta}{r^2}}=cos \theta sin\theta
因为 \theta取任意值(代表任意趋近路径),极限值就不一样,所以,极限不存在。
再举一例:I_{3}=\lim_{(x,y) \rightarrow (0,0)}{\frac{xy}{x+y}}
辅导书解法:同样,令 y=kx,则
I_{3}=\lim_{(x,y) \rightarrow (0,0)}{\frac{xy}{x+y}}=\lim_{x \rightarrow 0}{\frac{kx^2}{(1+k)x}}=\lim_{x \rightarrow 0}{\frac{kx}{1+k}}=0
令人沮丧的是,极限是不存在的(别问我为什么知道不对)
取一个特别的趋近路径,即 y=\frac{-x}{1+x},则
I_{3}=\lim_{(x,y) \rightarrow (0,0)}{\frac{xy}{x+y}}=\lim_{x \rightarrow 0}{\frac{\frac{-x^2}{1+x}}{x+\frac{-x}{1+x}}}=\lim_{x \rightarrow 0}{\frac{\frac{-x^2}{1+x}}{\frac{x^2}{1+x}}}=-1
两条不同的趋近路径,结果分别是0和 -1 ,显然极限不存在!
我的解法:令 x=rcos\theta ,y=rsin\theta,则
I_{3}=\lim_{(x,y) \rightarrow (0,0)}{\frac{xy}{x+y}}=\lim_{r \rightarrow 0^+}{\frac{r^2cos\theta sin\theta}{r(cos\theta+sin\theta)}}=\lim_{r \rightarrow 0^+}{\frac{rcos\theta sin\theta}{(cos\theta+sin\theta)}}
因为 \theta取任意值(代表任意趋近路径),我们不妨取\theta=\frac{3\pi}{4},则 I_{3}=\infty,显然极限不存在!
- I_{s1}=\lim_{(x,y) \rightarrow 0,0}{\frac{xy^2sinky}{x^2+y^4}},k为常数
解法一(夹逼准则): \left| \frac{xy^2sinky}{x^2+y^4} \right|\leq\left| \frac{xy^2}{2xy^2} \right|\left| sinky \right|=\frac{1}{2}\left| sinky \right|
取极限,知 I_{s1}=0 。
解法二(极坐标变换法):令 x=rcos\theta ,y^2=rsin\theta,y=\pm\sqrt{rsin\theta} , \theta\in(0,\pi) 则
I_{s1}=\lim_{r \rightarrow 0^+}{\frac{\pm r^2cos\theta sin\theta sink\sqrt{rsin\theta}}{r^2}}=\pm\lim_{r \rightarrow 0^+} sin[\sqrt{r}(k\sqrt{sin\theta})]cos\theta sin\theta=0
- I_{s2}=\lim_{(x,y) \rightarrow (0,0)}{\frac{sin(x^2y+y^4)}{x^2+y^2}}
解法一(夹逼准则): \left| {\frac{sin(x^2y+y^4)}{x^2+y^2}} \right|\leq\left| \frac{x^2y+y^4}{x^2+y^2} \right|=\left| \frac{x^2+y^3}{x^2+y^2} \right|\left| y \right|\leq\left| \frac{x^2+\left| y^3 \right|}{x^2+y^2} \right|\left| y \right|\leq\left| \frac{x^2+y^2 }{x^2+y^2} \right|\left| y \right|=\left| y \right|
取极限得I_{s2}=0 。
解法二(极坐标代换法):令 x=rcos\theta ,y=rsin\theta ,则
I_{s2}=\lim_{r \rightarrow 0^+}{\frac{sin(r^3cos^2\theta sin\theta+r^4sin^4\theta)}{r^2}}=\lim_{r \rightarrow 0^+}{\frac{r^3cos^2\theta sin\theta+r^4sin^4\theta+o(r^3cos^2\theta sin\theta+r^4sin^4\theta)}{r^2}}=\lim_{r \rightarrow 0^+}{rcos^2\theta sin\theta+r^2sin^4\theta}=0
<hr/>三、证明题
证明题是性价比最低的题型,其在考研中一般是作为压轴题出现的,难度极高,分值大概在10分左右,但这类题型要想完全掌握,创痛的放需要花费大量的方法,甚至即便花费大量时间,也有可能还是掌握不了。概因证明题存在思路壁垒,即便你对拉格朗日定理、泰勒公式、费马引理等等定理背的再透彻,也会被繁杂的不同组合题型搞晕头绪。证明题主要包括:
数列极限存在性证明、微积分等式(包括中值定理证明题、零点问题和微积分恒等式)、微积分不等式三大部分。
证明题的难度众所周知,很多同学是希望通过“遍历”的方式穷尽考研数学证明题的证明,并归纳出复杂的不同类型的中证明题,这种方式不可取,问题就在于,如果给出的证明题具有灵活性,你又无法从归纳的类型中找出对应的题目,那么,你就无法做了,甚至这种穷尽的归纳很难真的穷尽。
1.数列极限存在性证明题
而针对数列极限的存在性,我们给出四种解法——单调有界、压缩映射、双层单调有界和对比证明法,能够解决所有的数列极限存在性证明题;
2.微积分等式
针对微积分等式,我们给出图表法。
3.微积分不等式
针对微积分不等式,我们给出九点开图法。
如单调有界的数学归纳法(参照破天学长:单调有界准则考点的万能解法之一——数学归纳法):
设 a_{1}=5,a_{n}=5+\frac{6}{a_{n-1}},n=2... ,证明 \lim_{n \rightarrow \infty}{a_{n}} 存在并求极限值。
我们先写出前五项,从数值上分析一下数列的单调性!
a_{1}=5,a_{2}=5+\frac{6}{5},a_{3}=5+\frac{6}{5+\frac{6}{5}},a_{4}=5+\frac{6}{5+\frac{6}{5+\frac{6}{5}}},a_{5}=5+\frac{6}{5+\frac{6}{5+\frac{6}{5+\frac{6}{5}}}}\\
a_{1}=5,a_{2}=6.2,a_{3}\approx5.97,a_{4}\approx6.01,a_{5}\approx5.99\\
显然, a_{1}<a_{2}>a_{3}<a_{4}>a_{5} ,单调性卒!(不相信的请自己用单调有界做一下!!当然也有别的做法,如压缩映像)
那是不是单调有界的数学归纳法就不能用了?
显然不是,我们做如下分析:
你会发现大于号和小于号是交替出现的,所以我们猜想,是不是分奇偶项有分别的单调性呢?(踏出这一步就足够了)
于是,a_{1}<a_{3}<a_{5}\\
a_{2}>a_{4}\\
可以看出来前五项中,奇数项单调递增,偶数项单调递减。那我们按照奇偶项分别使用单调有界准则的数学归纳法,尝试验证以下!
先给出奇数项偶项项的递推表达式,即
a_{n}=5+\frac{6}{5+\frac{6}{a_{n-2}}},(n=3,5...为奇数列;n=4,6...为偶数列)
- 确定取值范围:a_{1}=5,a_{n}>5,n=2...\\
- 先求极限值(并不代表极限值存在):A=5+\frac{6}{A}\\
A=6(A=-1舍去),A^2-5A-6=0\\
- (1)证奇数列的有界性(数学归纳法三连):a_{1}=5,a_{1}<6;\\
a_{k}<6;\\
a_{k+2}=5+\frac{6}{5+\frac{6}{a_{k}}}<6\\
所以奇数列有上界6.
(2)证偶数列的有界性(数学归纳法三连):a_{2}=6.2,a_{2}>6;\\
a_{k}>6;\\
a_{k+2}=5+\frac{6}{5+\frac{6}{a_{k}}}>6\\
所以偶数列有下界6.
- (1)证奇数列的单调性(数学归纳法三连)::a_{1}=5<a_{3}=5+\frac{6}{5+\frac{6}{5}};\\
a_{k}<a_{k+2};\\
a_{k+2}-a_{k+4}=\frac{6(a_{k}-a_{k+2})}{(5a_{k}+6)(5a_{k+2}+6)}<0;\\
a_{k+2}<a_{k+4}\\
所以奇数列单调递增。
(2)证偶数列的单调性(数学归纳法三连)::a_{2}=6.2>a_{4}=5+\frac{6}{5+\frac{6}{6.2}};\\
a_{k}>a_{k+2};\\
a_{k+2}-a_{k+4}=\frac{6(a_{k}-a_{k+2})}{(5a_{k}+6)(5a_{k+2}+6)}>0;\\
a_{k+2}>a_{k+4}\\
所以偶数列单调递减。
因为奇数列单调递增有上界,根据单调有界准则,其必有极限;同理,偶数列单调递增有下界,也必有极限。分别对奇数列和偶数列求极限可知极限值都是6。
再根据数列极限的充要条件可知,奇偶数列极限值存在且均等于A \Leftrightarrow 原数列极限存在且极限值为A。
故,数列极限值存在且为6。
11 |
|